2.3. Общий алгоритм Брезенхема

Хотя алгоритм Брезенхема был первоначально разработан для цифровых графопостроителей, однако он в равной степени подходит и для использования растровыми устройствами с ЭЛТ. Алгоритм выбирает оптимальные растровые координаты для представления отрезка. Большее из приращений, либо Δx, либо Δy, выбирается в качестве единицы растра.В процессе работы одна из координат (в зависимости от углового коэффициента) изменяется на единицу. Изменение другой координаты (на 0 или 1) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние мы назовем ошибкой.

Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис. 2.3 это иллюстрируется для отрезка в первом октанте, т. е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0, 0) больше чем ½,то его пересечение с прямой х = 1 будет расположено ближе к прямой y = 1, чем к прямой y = 0. Следовательно, точка растра (1, 1) лучше аппроксимирует ход отрезка, чем точка (1, 0). Если угловой коэффициент меньше ½, то верно обратное. Для углового коэффициента, равного ½, нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1, 1).

 

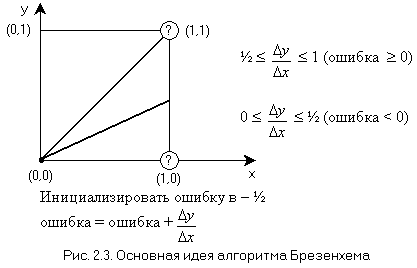
Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной -½. Таким образом, если угловой коэффициент отрезка больше или равен ½, то величина ошибки в следующей точке растра может быть вычислена как е = -½ + Δy/Δx. Недостаток такого вычисления ошибки в том, что она требует использования арифметики с плавающей точкой и деления для вычисления углового коэффициента. Быстродействие алгоритма можно увеличить, если использовать только целочисленную арифметику и исключить деление. Простое преобразование ē = (-½ + Δy/Δx) · 2Δx = 2Δy - Δx превратит предыдущие вычисления в целочисленные и позволит эффективно реализовать их на аппаратном или микропрограммном уровне.

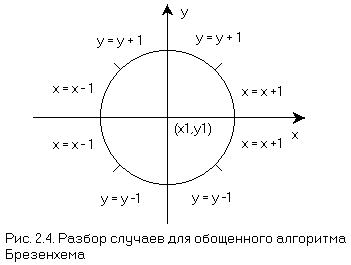
Чтобы реализация алгоритма Брезенхема была полной, необходимо обрабатывать отрезки во всех октантах. Это легко сделать, учитывая в алгоритме номер квадранта, в котором лежит отрезок и его угловой коэффициент. Когда абсолютная величина углового коэффициента больше 1, y постоянно изменяется на единицу, а критерий ошибки Брезенхема используется для принятия решения об изменении величины x. Выбор постоянно изменяющейся (на +1 или -1) координаты зависит от квадранта (рис. 2.4).

 

Общий алгоритм может быть оформлен в следующем виде:

Обобщенный целочисленный алгоритм Брезенхема квадрантов.
Sign (x) - возвращает -1, 0, 1 для отрицательного, нулевого и положительного аргумента соответственно.

 

х = x1; y = y1; Dх = abs(x2 - х1); Dу = abs(y2 - у1); s1 = Sign(х2 - х1); s2 = Sign(y2 - y1);	/ инициализация переменных
If Dу > Dх then Врем = Dх; Dх = Dу; Dу = Врем; Обмен = 1; else Обмен = 0; end if	/ обмен значений Δx и Δy в зависимости от углового коэффициента наклона отрезка
ē = 2Dy - Dx;	/ инициализация ē с поправкой на половину пиксела
for i = 1 to Dх Plot(x,y); while (е >= 0) If Обмен = 1 then x = x + s1; else y = y + s2; end if ē = ē - 2Dх; end while If Обмен = 1 then y = y + s2; else x = x + s1; end If ē = ē + 2Dy; next i finish	/ основной цикл

Пример 2.1. Обобщенный алгоритм Брезенхема
Для иллюстрации общего алгоритма Брезенхема рассмотрим отрезок из точки (0,0) в точку (-8, -4):
x1 = 0
у1 = 0
х2 = 8
y2 = 4
s1 = -1
s2 = -1
Обмен = 0
ē = 0
Результаты пошагового исполнения основного цикла:

 

i 1 2 3 4 5 6 7 8

Plot (0, 0) (-1, -1) (-2, -1) (-3, -2) (-4, -2) (-5, -3) (-6, -3) (-7, -4)

ē 0 -16 -8 0 -16 -8 0 -16 -8 0 -16 -8 0

x 0 0 -1 -2 -2 -3 -4 -4 -5 -6 -6 -7 -8

y 0 -1 -1 -1 -2 -2 -2 -3 -3 -3 -4 -4 -4

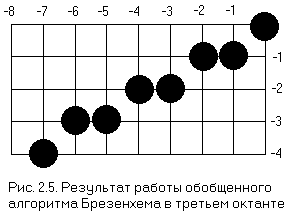
На рис. 2.5 продемонстрирован результат.