2.5. Растровая развертка сплошных областей
Для сих пор речь шла о представлении на растровом графическом устройстве отрезков прямых линий. Однако одной из уникальных характеристик такого устройства является возможность представления сплошных областей. Генерацию сплошных областей из простых описаний ребер или вершин будем называть растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на две широкие категории: заполнение в порядке сканирования строк и затравочное заполнение.
В первом случае пытаются определить в порядке сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно идут от "верха" многоугольника или контура к "низу". Этот метод развертки также применим и к векторным дисплеям, в которых он используется для штриховки или закраски контуров.
В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если соседняя точка расположена не внутри, значит, обнаружена граница контура. Если же точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно. Подобные алгоритмы применимы только к растровым устройствам.
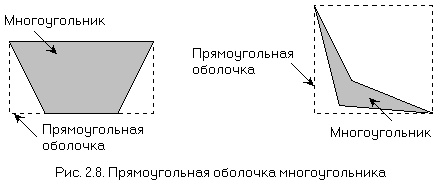
Многие замкнутые контуры являются простыми многоугольниками. Если контур состоит из кривых линий, то его можно аппроксимировать подходящим многоугольником или многоугольниками. Простейший метод заполнения многоугольника состоит в проверке на принадлежность внутренности многоугольника каждого пиксела в растре. Так как обычно большинство пикселов лежит вне многоугольника, то данный метод слишком расточителен. Затраты можно уменьшить путем вычисления для многоугольника прямоугольной оболочки - наименьшего прямоугольника, содержащего внутри себя многоугольник. Как показано на рис. 2.9, проверяются только внутренние точки этой оболочки. Использование прямоугольной оболочки для многоугольника, изображенного на рис. 2.9,а, намного сокращает число проверяемых пикселов. В то же время для многоугольника, представленного на рис. 2.9,b, сокращение существенно меньше.