2.6. Заполнение многоугольника в порядке сканирования строк

Можно разработать более эффективный тест на принадлежность внутренней части, если воспользоваться тем фактом, что соседние пикселы, вероятно, имеют одинаковые характеристики (кроме пикселов граничных ребер). Это свойство называется пространственной когерентностью. Для растровых графических устройств соседние пикселы на сканирующей строке, вероятно, имеют одинаковые характеристики. Это когерентность растровых строк.

Тест принадлежности точки многоугольнику
Обозначим ребра простого многоугольника на рис. 2.10. P₁P₂, P₂P₃, ..., P_nP₁. Пусть A(x, y) - точка, не лежащая на ломаной и нужно определить, принадлежит она многоугольнику или нет.

 

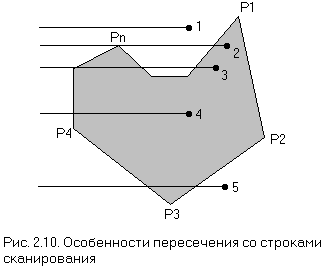
Проведем через точку горизонтальную полупрямую с правым концом в точке. Отметим на ней точку Q, которая заведомо не принадлежит многоугольнику.

В результате возникают следующие варианты:

1. Нет пересечений с многоугольником ==> точка А внешняя (точка 1).
2. Нечетное число пересечений ==> точка А внутренняя (точки 3 и 4).
3. Четное число пересечений ==> точка А внешняя (точка 5).

Следует отметить, что горизонтальные ребра не могут пересекать сканирующую строку и поэтому игнорируются. Дополнительная трудность возникает при пересечении сканирующей строки и многоугольника точно по вершине (точка 2). Правильный результат можно получить, учитывая точку пересечения в вершине два раза, если она является точкой локального минимума или максимума и учитывая ее один раз в противном случае. Определить локальный максимум или минимум многоугольника в рассматриваемой вершине можно с помощью проверки концевых точек двух ребер, соединенных в вершине. Если у обоих концов координаты y больше, чем у вершины, значит, вершина является точкой локального минимума. Если меньше, значит, вершина - точка локального максимума. Если одна больше, а другая меньше, следовательно, вершина не является ни точкой локального минимума, ни точкой локального максимума. На рис. 2.10 Р3 - локальный минимум, Р1 - локальный максимум, а Р2, Р4, ..., Pn - ни то и ни другое. Следовательно, в точках Р1 и P3 учитываются два пересечения со сканирующими строками, а в Р2, P4, ..., Pn - одно.

Алгоритм заполнения многоугольника в порядке сканирования строк заключается в том, что многоугольник, разбивает всякую горизонтальную прямую на чередующаяся интервалы, лежащие внутри и снаружи многоугольника. Зафиксируем эту горизонтальную прямую на конкретном уровне. Найдем точки пересечения, если они есть, этой прямой и каждого ребра многоугольника. Совсем необязательно, чтобы точки пересечения для строки сразу определялись в фиксированном порядке (слева направо). Эти точки затем можно отсортировать в возрастающем порядке по х и разбить по парам.

При определении интенсивности, цвета и оттенка пикселов на сканирующей строке рассматриваются пары отсортированных точек пересечений. Для каждого интервала, задаваемого парой пересечений, используется интенсивность или цвет заполняемого многоугольника. Для интервалов между парами пересечений и крайних (от начала строки до первой точки пересечения и от последней точки пересечения до конца строки) используется фоновая интенсивность или цвет.

Точное определение тех пикселов, которые должны активироваться, требует некоторой осторожности. Рассмотрим простой прямоугольник, изображенный на рис. 2.11. Прямоугольник имеет координаты (1,1) (5,1), (5,4), (1,4). Сканирующие строки с 1 по 4 имеют пересечения с ребрами многоугольника при х = 1 и 5. Вспомним, что пиксел адресуется координатами своего левого нижнего угла, значит, для каждой из этих сканирующих строк будут активированы пикселы с x-координатами 1, 2, 3, 4 и 5. На рис. 2.11,а показан результат. Заметим, что площадь, покрываемая активированными пикселами, равна 20, в то время как настоящая площадь прямоугольника равна 12.

 

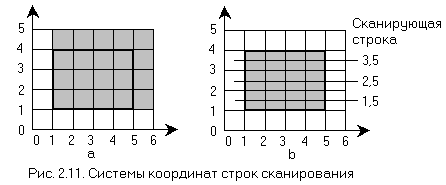
Модификация системы координат сканирующей строки и теста активации устраняет эту проблему, как это показано на рис. 2.11,b. Считается, что сканирующие строки проходят через центр строк пикселов, т. е. через середину интервала, как это показано на рис. 2.11,b. Тест активации модифицируется следующим образом:проверяется, лежит ли внутри интервала центр пиксела, расположенного справа от пересечения. Однако пикселы все еще адресуются координатами левого нижнего угла. Как показано на рис. 2.11,b, результат данного метода корректен. Перебирая все линии сверху вниз, мы получим заполнение в порядке сканирования строк.

Алгоритм можно улучшить, если повысить эффективность сортировки. Последнее достигается разделением сортировки по строкам в направлении y и сортировки в строке в направлении x с помощью групповой сортировки по y. Таким образом, развертка начинается до завершения всего процесса сортировки.