2.8. Построчный алгоритм заполнения с затравкой

Как видно из предыдущего примера, стек может стать довольно большим. Еще один недостаток предыдущего алгоритма - стек зачастую содержит дублирующую или ненужную информацию. В построчном алгоритме заполнения с затравкой размер стека минимизируется за счет хранения только одного затравочного пиксела для любого непрерывного интервала на сканирующей строке. Непрерывный интервал - это группа примыкающих друг к другу пикселов (ограниченная уже заполненными или граничными пикселами). Мы для разработки алгоритма используем эвристический подход, однако также возможен и теоретический подход, основанный на теории графов.

Данный алгоритм применим к гранично-определенным областям. Гранично-определенная 4-связная область может быть как выпуклой, так и не выпуклой, а также может содержать дыры. В области, внешней и примыкающей к нашей гранично-определенной области, не должно быть пикселов с цветом, которым область или многоугольник заполняется. Схематично работу алгоритма можно разбить на четыре этапа.

Построчный алгоритм заполнения с затравкой

1. Затравочный пиксел на интервале извлекается из стека, содержащего затравочные пикселы.
2. Интервал с затравочным пикселом заполняется влево и вправо от затравки вдоль сканирующей строки до тех пор, пока не будет найдена граница.
3. В переменных Х_лев и Х_прав запоминаются крайний левый и крайний правый пикселы интервала.
4. В диапазоне Х_лев <= x <= X_прав проверяются строки, расположенные непосредственно над и под текущей строкой. Определяется, есть ли на них еще не заполненные пикселы. Если такие пикселы есть (т. е. не все пикселы граничные, или уже заполненные), то в указанном диапазоне крайний правый пиксел в каждом интервале отмечается как затравочный и помещается в стек.
5. При инициализации алгоритма в стек помещается единственный затравочный пиксел, работа завершается при опустошении стека.

Как показано в примере ниже, алгоритм справляется с дырами и зубцами на границе. Ниже приводится более подробное описание алгоритма на псевдокоде:

Затравка (х,у) - выдает затравочный пиксел
Pop - процедура, которая извлекает пиксел из стека
Push - процедура, которая помещает пиксел в стек

 

Push Затравка (х, у) while (стек не пуст)	/ инициализируем стек
Pop Пиксел (х, у) Пиксел (х, у) = Нов_значение	/ извлекаем пиксел из стека и присваиваем ему новое значение
Врем_х = х	/ сохраняем x-координату затравочного пиксела
х = х + 1 while Пиксел (х, у) <> Гран_значение Пиксел (х, у) = Нов_значение х = х + 1 end while	/ заполняем интервал справа от затравки
Хправ = х — 1	/ сохраняем крайний справа пиксел
х = Врем_х	/ восстанавливаем х-координату затравки
х = х — 1 while Пиксел (х, у) <> Гран_значение Пиксел (х, у) = Нов_значение х = х — 1 end while	/ заполняем интервал слева от затравки
Хлев = х + 1	/ сохраняем крайний слева пиксел
х = Врем_х	/ восстанавливаем х-координату затравки
х = Хлев у = у + 1 while х <= Хправ	/ проверим, что строка выше не является ни границей мно- гоугольника, ни ухе полностью заполненной; если это не так, то найти затравку, начиная с левого края подынтер- вала сканирующей строкивосстанавливаем х-координату затравки
Флаг = 0 while (Пиксел (х, у) <> Гран_значение and Пиксел (х, у) <> Нов_значение and х < Хправ if Флаг = 0 then Флаг = 1 x = x + 1 end while	/ ищем затравку на строке выше
if Флаг = 1 then if (x = Хправ and Пиксел (х, у) <> Гран_значение and Пиксел (х, у) <> Нов_значение) then Push Пиксел (х, у) elsePush Пиксел (х — 1, у) end if Флаг = 0 end If	/ помещаем в стек крайний справа пиксел
Хвход = х while ((Пиксел (х, у) = Гран_значение оr Пиксел (х, у) = Нов_значение) and х < Хправ) х = х + 1 end while	/ продолжим проверку, если интервал был прерван
if х = Хвход then х = х + 1 end while	/ удостоверимся, что координата пиксела увеличена
эта часть алгоритма совершенно аналогична проверке для строки выше, за исключением того, что вместо y = y + 1 надо подставить y = y — 1 end while finish	/ проверим, что строка ниже не является ни границей многоугольника, ни уже полностью заполненной

Пример 2.4. Построчный алгоритм заполнения с затравкой.
Рассмотрим работу алгоритма для гранично-определенной области на рис. 2.16. При инициализации в стек помешается затравочный пиксел, помеченный как Затравка (5,7) на рис. 2.16,а. Первоначально в качестве затравки интервала из стека извлекается этот пиксел. Интервал заполняется справа и слева от затравки. Найденные при этом концы интервала Х_прав = 9 и X_лев = 1. Затем проверяется строка, расположенная выше текущей и оказывается, что она не граничная и не заполненная. Крайним правым пикселом в диапазоне 1 <= x <= 9 оказывается пиксел (8,8), помеченный цифрой 1 на рис. 2.16,а. Этот пиксел помещается в стек. Затем аналогичным образом обрабатывается строка ниже текущей. В диапазоне Х_лев <= x <= X_прав есть два подинтервала на этой стороне. Для левого интервала в качестве затравки выступает пиксел (3,6), помеченный цифрой 2 на рис. 2.16,а, он тоже помещается в стек. Затравка для правого подинтервала - пиксел (9,6), он помещается в стек. Заметим, что пиксел (9,6) - не самый крайний правый пиксел на интервале, однако это самый крайний правый пиксел в диапазоне Х_лев <= x <= X_прав, т.е. в диапазоне 1 <= x <= 9. На этом завершается первый проход алгоритма.

 

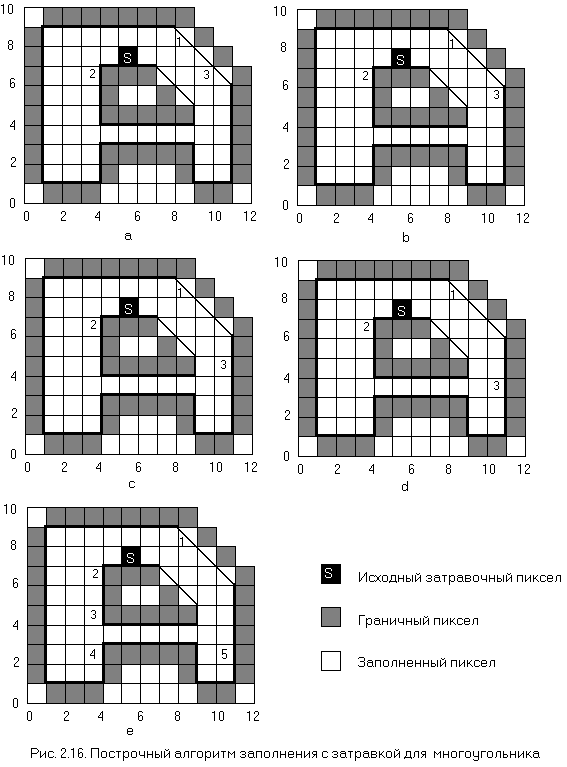
Далее из стека извлекается верхний пиксел. Здесь заполняются интервалы, расположенные в правой части многоугольника на последовательных сканирующих строках (рис. 2.16, b, c, d). Для строки 3 затравкой служит пиксел (10,3) (рис. 2.16, d). В результате заполнения интервала справа и слева от затравки получаем новые пределы диапазона Х_прав = 10 и X_лев = 1. Обрабатывая строку выше, получаем для основного подынтервала затравочный пиксел (3,4), коорый помещается в стек. Правый подинтервал к этому времени уже заполнен. Обработка строки ниже дает затравку (3,2) для левого и (10,2) для правого подынтервалов. Эти пикселы также помещаются в стек. Именно сейчас достигается максимальная глубина стека для обрабатываемого многоугольника.

Теперь остается только один интереснй момент. После заполнения 4-связных полигональных подобластей с затравочными пикселами 5, 4 и 3 на рис. 2.16,е из стека извлекается пиксел, помеченный цифрой 2. Здесь мы обнаруживаем, что все пикселы на этой строке уже и на соседних строках (выше и ниже) уже заполнены. Таким образом, ни один пиксел в стек не помещается. Из стека извлекается пиксел 1 и строка обрабатывается, при этом вновь добавочных пикселов не появляется. Теперь стек пуст, многоугольник заполнен и работа алгоритма завершена.

По сравнению с алгоритмом из разд. 2.7 максимальная глубина стека в этом примере равна пяти.