2.10. Алгоритм Брезенхема с устранением ступенчатости

В алгоритмах разложения отрезка в растр и заполнения многоугольника, обсуждавшихся выше, интенсивность или цвет пиксела определялись интенсивностью или цветом единственной точки внутри области пиксела. В этих методах предполагалось, что пиксел является скорее математической точкой, нежели конечной областью. В методах растровой развертки сплошной области, тоже обсуждавшихся выше, определение местоположения пиксела (внутри или вне многоугольника) основывалось на положении центра пиксела. Если центр находился внутри, то активировался весь пиксел. Если центр находился вне, то игнорировалась вся область пиксела. Этот метод необходим для простых двухуровневых изображений, т. е. черных или белых, цвета многоугольника или цвета фона. В результате получается характерное ступенчатое или зазубренное ребро многоугольника или отрезок. Как обсуждалось в предыдущем разделе, основной причиной лестничного эффекта является то, что дискретность отрезка или ребра недостаточна для того, чтобы соответствовать дискретным пикселам экрана дисплея.

При наличии нескольких интенсивностей, т. е. полутонов серого или оттенков цвета, внешний вид ребра или отрезка может быть улучшен размыванием краев. Простой эвристический метод состоит в том, чтобы устанавливать интенсивность пиксела на ребре пропорционально площади части пиксела, находящейся внутри многоугольника. Эта простая форма устранения ступенчатости иллюстрируется на рис. 2.19, на котором изображено одно ребро многоугольника с тангенсом угла наклона 5/8. Внутренняя часть многоугольника расположена справа. На рис. 2.19,а представлено ребро, разложенное в растр с помощью стандартного алгоритма Брезенхема с использованием только двух уровней интенсивности. Изображение имеет характерный зазубренный или ступенчатый вид. На рис. 2.19,b для выбора одного из восьми (от 0 до 7) уровней интенсивности используется площадь части пиксела, находящейся внутри многоугольника. Заметим, что так как эта площадь для некоторых пикселов меньше одной восьмой, то некоторые пикселы, полностью черные на рис. 2.19,а, окрашены в белый цвет на рис. 2.19,b.

 

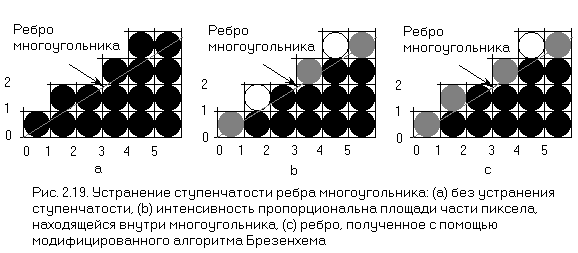
В результате простой модификации алгоритма Брезенхема можно получить аппроксимацию площади части пиксела, находящейся внутри многоугольника. Эту аппроксимацию можно использовать для модуляции интенсивности. Как показано на рис. 2.20, при пересечении пиксела и отрезка с тангенсом угла наклона m (0 <= m <= 1) может быть задействован либо один, либо два пиксела. Если пересекается только один пиксел (рис. 2.20,а), то площадь правее и ниже отрезка равна y_i + m/2. Если же надо рассмотреть два пиксела (рис. 2.20,b), то площадь нижнего пиксела составляет 1 - (1 - y_i)²/2m, а верхнего - (у_i - 1 + m)²/2m. Для отрезка в первом октанте с тангенсом угла наклона 0 <= m <= 1 площадь верхнего пиксела может быть достаточно мала для того, чтобы ее можно было проигнорировать в вышеописанном эвристическом методе, например, для пиксела (1, 1) на рис. 2.19,b. Однако объединение этой площади с площадью нижнего пиксела позволит более реалистично представить ребро многоугольника. Суммарная площадь для двух пикселов равная, y_i + m/2.

 

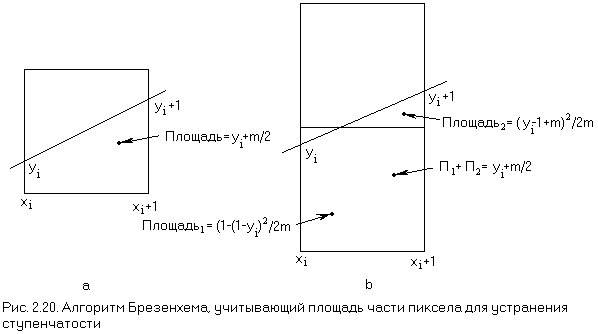
Если к ошибке в исходном алгоритме Брезенхема добавить величину w = 1 - m, т. е. ввести преобразование  ē = е + w, то 0 <= ē <= 1. Теперь ошибка ē - это мера площади той части пиксела, которая находится внутри многоугольника, т. е. у_i + m/2. В связи с этими модификациями начальное значение ошибки равно ½ поэтому для первого пиксела алгоритм всегда будет выдавать значение интенсивности, равное половине максимальной. Более реалистичное значение для первого пиксела дает перемещение оператора активирования пиксела на другое место. Более того, можно получить непосредственно значение интенсивности, а не десятичную дробь от ее максимума с помощью умножения на максимальное число доступных уровней интенсивности I следующих величин: тангенса угла наклона (m), весового коэффициента (w) и ошибки ē. Модифицированный алгоритм выглядит следующим образом:

Модифицированный алгоритм Брезенхема с устранением ступенчатости для первого квадранта
отрезок проводится из (х₁, y₁) в (х₂, y₂)
I - число доступных уровней интенсивности
переменные целого типа

 

х = х1 y = y1 Δх = х2 - x1 Δy = y2 - y1	/ инициализация переменных
m = (I · Δy)/Δх w = I - m ē = 1/2 Plot (x, y, m/2) while (x < x2) If ē < w then x = x + 1 ē = ē + m else x = x + 1 y = y + 1 ē = ē - w end if Plot (x, y, ē) end while finish

Интенсивность для первого пиксела предполагает, что отрезок начинается с адреса пиксела.Результаты для отрезка с тангенсом угла наклона m = 5/8 и восемью уровнями интенсивности представлены на рис. 2.19,с. Распространить работу алгоритма на другие октанты можно тем же способом, что и для основного алгоритма Брезенхема.