3.1. Двумерное отсечение

Отсечение, т. е. процесс выделения некоторой части базы данных, играет важную роль в задачах машинной графики. Отсечение применяется в алгоритмах удаления невидимых линий и поверхностей, при построении теней, а также при формировании фактуры. Алгоритмы отсечения бывают дву- или трехмерными и применяются как к регулярным (прямоугольники и параллелепипеды со сторонами, параллельными осям координат), так и к нерегулярным областям и объемам.

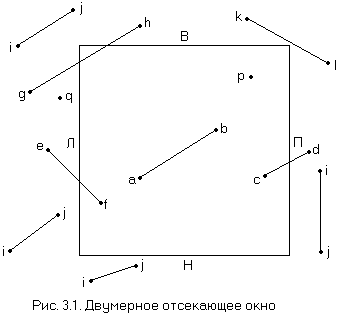
На рис. 3.1 показана плоская сцена и отсекающее окно регулярной формы. Окно задается левым (Л), правым (П), верхним (В) и нижним (Н) двумерными ребрами. Регулярным отсекающим окном является прямоугольник, стороны которого параллельны осям координат объектного пространства или осям координат экрана. Целью алгоритма отсечения является определение тех точек, отрезков или их частей, которые лежат внутри отсекающего окна. Эти точки, отрезки или их части остаются для визуализации. А все остальное отбрасывается.

Поскольку в обычных сценах или картинках необходимо отсекать большое число отрезков или точек, то эффективность алгоритмов отсечения представляет особый интерес. Во многих случаях подавляющее большинство точек или отрезков лежит целиком внутри или вне отсекающего окна. Поэтому важно уметь быстро отбирать отрезки, подобные ab, или точки, подобные р, и отбрасывать отрезки, подобные ij, или точки, подобные q на рис. 3.1.

 

Точки, лежащие внутри отсекающего окна, удовлетворяют условию: x_л <= х <= x_п, y_н <= y <= y_в. Знак равенства здесь показывает, что точки, лежащие на границе окна, считаются находящимися внутри него.

Отрезок лежит внутри окна и, следовательно, является видимым, если обе его концевые точки лежат внутри окна, например отрезок ab на рис. 3.1. Однако если оба конца отрезка лежат вне окна, то этот отрезок не обязательно лежит целиком вне окна, например отрезок gh на рис. 3.1. Если же оба конца отрезка лежат справа, слева, выше или ниже окна, то этот отрезок целиком лежит вне окна, а значит, невидим. Проверка последнего условия устранит все отрезки, помеченные ij на рис. 3.1. Но она не устранит ни отрезка gh, который видим частично, ни отрезка kl, который целиком невидим.

Пусть а и b - концы отрезка, тогда можно предложить алгоритм, определяющий все полностью видимые и большинство невидимых отрезков:

Простой алгоритм определения видимости
a, b - концевые точки отрезка в координатном пространстве (х, у)

 

	для каждого отрезка проверить полную видимость отрезка если одна из координат какого-нибудь конца отрезка находится вне окна, то отрезок не является полностью видимым if хa < хл оr хa > хп then 1 if хb < хл оr хb > хп then 1 if ya < yн оr ya > yв then 1 if yb < yн оr yb > yв then 1 отрезок полностью видимый визуализировать отрезок go to 3 проверить полную невидимость отрезка если оба конца отрезка лежат слева, справа, сверху или снизу от окна, то факт невидимости отрезка тривиален
1	if хa < хл and хb < хл then 2 if хa > хп and хb > хп then 2 if ya > yв and yb > yв then 2 if ya < yн and yb < yн then 2 отрезок частично видим или пересекает продолжение диагонали, оставаясь невидимым определить пересечения отрезка с окном
2	отрезок невидим
3	переход к следующему отрезку

Пересечение двух отрезков можно искать как параметрическим, так и непараметрическим способами. Очевидно, что уравнение бесконечной прямой, проходящей через точки Р₁(х₁, y₁) и Р₂(х₂,y₂), имеет вид y = m(х - х₂) + y₂ или у = m(х - х₂) + у₂, где m = (y₂ - y₁)/ (х₂ - х₁) - это наклон данной прямой. Точки пересечения этой прямой со сторонами окна имеют следующие координаты:

с левой: хл, y = m(хл - х1) + y1 с правой: хп, y = m(хп - х1) + y1 с верхней: yв, х = х1 + (1/m)(yв - y1)      с нижней: yн, х = х1 + (1/m)(yн - у1)

m <> бесконечность m <> бесконечность m <> 0 m <> 0

Чтобы разработать схему эффективного алгоритма отсечения, необходимо сначала рассмотреть несколько частных случаев. Если наклон отрезка бесконечен, то отрезок параллелен левой и правой сторонам окна и надо искать его пересечения только с верхней и нижней сторонами. Аналогично, если наклон равен нулю, то отрезок параллелен верхней и нижней сторонам окна, а искать его пересечения надо только с левой и правой сторонами.