3.4. Алгоритм Кируса-Бека

Для создания надежного алгоритма отсечения нужно иметь хороший метод определения местоположения относительно окна (внутри, на границе или вне его) точки, принадлежащей отрезку. Для этой цели в алгоритме Кируса-Бека используется вектор нормали.

 

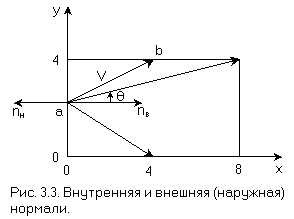
Возьмем выпуклую отсекающую область R. Хотя R не обязана быть двумерной, в примерах, приведенных в данном разделе, предполагается, что она двумерна. Итак, R может быть любым плоским выпуклым многоугольником. Она не должна быть вогнутым многоугольником. Внутренняя нормаль n в произвольной точке а, лежащей на границе R, удовлетворяет условию: n · (b - а) >= 0, где b - любая другая точка на границе R. Чтобы убедиться в этом, вспомним, что скалярное произведение двух векторов V₁ и V₂ равно: V₁V₂ · |V₁||V₂| · cos θ, где θ - это меньший из двух углов, образованных V₁ и V₂. Заметим, что если θ = π/2, то cos θ = 0 и V₁ · V₂ = 0, т. е. когда скалярное произведение пары векторов равно нулю, то они перпендикулярны. На рис. 3.3 показана выпуклая область R, т. е. отсекающее окно. Там же показаны внешняя (наружная) n_н и внутренняя n_в нормали к границе окна, исходящие из точки а, лежащей на этой границе. Кроме того, на рис. 3.3 показаны еще несколько векторов, проведенных из точки а в другие точки на границе окна. Угол между n_в и любым из таких векторов всегда принадлежит интервалу -π/2 <= θ <= π/2. При таких значениях угла косинус его всегда положителен. Следовательно, положительно и скалярное произведение этих векторов, как было установлено выше. А вот угол между внешней нормалью и любым из подобных векторов равен π - θ, a cos (π - θ) = - cosθ при этом отрицателен.

Возвращаясь к определению пересечения отрезка со стороной окна, вновь возьмем параметрическое представление отрезка Р₁Р₂:

P(t) = Р1 + (Р2 - Р1)t,     0 <= t <= 1.

Пусть f - граничная точка выпуклой области R, а n — внутренняя нормаль к одной из ограничивающих эту область плоскостей. Тогда для любой конкретной величины t, т. е. для любой точки отрезка Р₁Р₂, из условия, что скалярное произведение внутренней нормали на вектор, начинающийся в произвольной точке отрезка и заканчивающийся в другой точке, лежащей на той же границе окна n · [P(t) - f] < 0 следует, что вектор P(t) - f направлен вовне области R. Из условия n · [P(t) - f] = 0 следует, что P(t) - f принадлежит плоскости, которая проходит через f и перпендикулярна нормали. Из условия n · [P(t) - f] > 0 следует, что вектор P(t) - f направлен внутрь R. Из всех этих условий взятых вместе следует, что бесконечная прямая пересекает замкнутую выпуклую область, которая в двумерном случае сводится к замкнутому выпуклому многоугольнику ровно в двух точках. Далее, пусть эти две точки не принадлежат одной граничной плоскости или ребру. Тогда уравнение n · [Р(t) - f] = 0 имеет только одно решение. Если точка f лежит на той граничной плоскости или на том ребре, для которых n является внутренней нормалью, то точка на отрезке Р(t), которая удовлетворяет последнему уравнению, будет точкой пересечения этого отрезка с указанной граничной плоскостью. Ниже приводится запись этого алгоритма на псевдокоде.

Алгоритм двумерного отсечения Кируса-Бека
Р₁,Р₂ - концевые точки отрезка
k - число сторон отсекающего окна
n_i - вектор нормали к i-й стороне окна
f_i - точка, лежащая на i-й стороне окна
D - директриса отрезка, равная Р₂ - Р₁
w_i - весовая функция, равная Р₁ - f_i
t_н, t_в - нижний и верхний пределы значений параметра t

 

	tн = 0 tв = 1	/ инициализируем пределы значений параметра, предполагая что отрезок полностью видимый
	D = Р2 - Р1	/ вычисляем директрису D
	for i = 1 to k	/ основной цикл
	wi = Р1 - fi call Скал-произвед(D,ni;Dск) call Скал-произвед(wi,ni;Wск)	/ вычисляем wi, D·ni и wi·ni для данного i
	if Dск = 0 then 2	/ отрезок вырождается в точку?
	t = -Wск / Dск	/ отрезок невырожден, вычислить t
	if Dск > 0 then 1	/ поиск верхнего и нижнего пределов t
	if t < 0 then 4 tв = min(t,tв) go to 3	/ поиск верхнего предела; верно ли, что 0 <= t <= 1?
1	if t > 1 then 4 tл = max(t,tл) go to 3	/ поиск нижнего предела; верно ли, что t <= 1?
2	if Wск < 0 then 4	/ отрезок выродился в точку
3	next i	/ точка видима относительно текущей границы
	if tн > tв then 4	/ произошел нормальный выход из цикла; проверка фактической видимости отрезка
	Начертить отрезок от Р(tн) до P(tв)
4	Обработать следующий отрезок
подпрограмма вычисления скалярного произведения
subroutine Скал-произвед(Вектор1,Вектор2;Скал)
Скал = Вектор1х · Вектор2х + Вектор1y · Вектор2y
return