3.5. Трехмерное отсечение
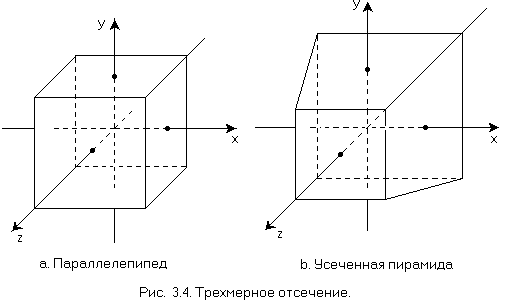
Прежде чем заняться обобщением изложенных методов для случая трех измерений, необходимо обсудить вопрос о форме отсекающего объема. Двумя наиболее распространенными формами трехмерных отсекателей являются: прямоугольный параллелепипед, т. е. полый брусок, используемый при параллельном или аксонометрическом проецировании, а также усеченная пирамида, часто называемая пирамидой видимости, которая используется при центральном проецировании. Эти формы показаны на рис. 3.4, у каждой из них шесть граней: левая, правая, верхняя, нижняя, ближняя и дальняя. Существует, кроме того, необходимость отсекать и по нестандартным объемам.
Как и при двумерном отсечении, отрезки, которые полностью видимы или тривиально невидимы, можно идентифицировать с использованием обобщения кодов концевых точек Коэна-Сазерленда. В трехмерном случае используется 6-битовый код. Вновь самый правый бит кода считается первым. В биты кода заносятся единицы с помощью обобщения двумерной процедуры. Конкретно единица заносится:
в первый бит - если конец ребра левее объема,
во второй бит - если конец ребра правее объема,
в третий бит - если конец ребра ниже объема,
в четвертый бит - если конец ребра выше объема,
в пятый бит - если конец ребра ближе объема,
в шестой бит - если конец ребра дальше объема.
В противном случае в соответствующие биты заносятся нули. И опять, если коды обоих концов отрезка равны нулю, то оба конца видимы и отрезок тоже будет полностью видимым. Точно так же, если побитовое логическое произведение кодов концов отрезка не равно нулю, то он полностью невидим. Если же это логическое произведение равно нулю, то отрезок может оказаться как частично видимым, так и полностью невидимым. В этом случае необходимо определять пересечения отрезка с гранями отсекающего объема.
Поиск кодов точки относительно отсекающего прямоугольного параллелепипеда является прямым обобщением соответствующего двумерного алгоритма. Однако случай, когда отсекателем служит усеченная пирамида, показанная на рис. 3.4, заслуживает дополнительного обсуждения. Один из методов заключается в преобразовании отсекателя в каноническую форму, где хправ = 1, хлев = 1, yверх = 1, yниз = - 1 при zдаль = 1. Если zближ = а, где 0 <= a <= 1, а центр проекции совпадает с началом левой системы координат, то проверка кодов концевых точек заметно упрощается.
Для трехмерного случая используется те же алгоритмы, что и для двумерного, только с небольшими коррективами. Так двумерный алгоритм разбиения средней точкой непосредственно обобщается на случай трех измерений. В записи этого алгоритма на псевдокоде нужно изменить размерности у нескольких массивов, а подпрограммы определения взаимного расположения точки и области отсечения переписать с учетом трех измерений.
В трехмерном алгоритме Кируса-Бека k обозначает не число сторон многоугольника, а число граней много гранника. Все векторы теперь имеют по три компоненты: х, у, z. Обобщение подпрограммы Скал-произвед на случай трехмерных векторов реализуется также непосредственно.