1.6. Масштабирование
Из наших рассуждений относительно преобразования точек следует, что величина масштабирования определяется значением элементов исходной диагональной матрицы. Если матрица
 |
 |
||
| [T] = |   |
2 0 0 2 |
 |
 |
 |
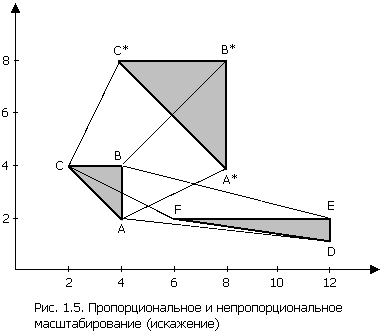
используется в качестве оператора воздействия на вершины треугольника, то имеет место «двукратное» расширение или равномерное масштабирование относительно точки начала координат. Если значения элементов не равны, то треугольник искажается, что проиллюстрировано на рис.1.5. Треугольник ABC, преобразованный с помощью матрицы
 |
 |
||
| [T] = |   |
2 0 0 2 |
  |
 |
 |
переходит в пропорционально увеличенный треуголник A*B*C*. Тот же треугольник, но преобразованный с помощью матрицы
|
переходит в треугольник DEF, имеющий искажение, вызванное разными коээфициентами масштабирования.
В общем случае при матрице
 |
 |
||
| [T] = |   |
a b c d |
  |
 |
 |
в которой а = d, b = с = 0, выполняется пропорциональное масштабирование; если a <> d, b = с = 0, то масштабирование будет проведено непропорционально. В первом случае для а = d > 1 происходит расширение, т.е. - увеличение изображения. Если а = d < 1, то происходит равномерное сжатие, т.е. фигура уменьшается. Непропорциональное расширение и сжатие возникают в зависимости от значений a и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.