1.8. Преобразование единичного квадрата

До сих пор мы рассматривали поведение точек и линий для определения результатов простых матричных преобразований. Однако можно корректно рассматривать применение матрицы к любой точке плоскости. Как было показано ранее, единственная точка, остающаяся инвариантной при воздействии матричных преобразований, - это точка начала координат. Все другие точки плоскости подвержены преобразованию, которое можно представить как растяжение исходной плоскости, системы координат и перевод в новую форму. Формально принято считать, что преобразование вызывает переход от одного координатного пространства к другому.

 

Рассмотрим координатную сетку, состоящую из единичных квадратов на координатной плоскости xy. Четыре координатных вектора вершин единичного квадрата, проходящие под одним углом к началу координат, имеют следующий вид:

 

A B C D		0   0   1   0   1   1   0   1

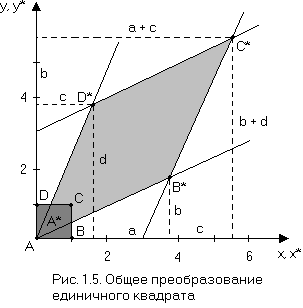
Такой единичный квадрат изображен на рис. 1.5. Применяя к нему (2х2) матрицу общего преобразования, получаем

 

	0   0   1   0   1   1   0   1			a   b   c   d	=		0         0   a         b   a + c   b + d   c         d

Результаты этого преобразования показаны на рис. 1.5. Из предыдущего выражения следует, что начало координат не подвергается преобразованию, т.е. [A] = [A*] = [0 0]. Далее отметим, что координаты B* равны первой строке матрицы преобразования, а координаты D* - второй. Таким образом, матрица преобразования является определенной, если определены координаты В* и D* (преобразование единичных векторов [1 0], [0 1]). Поскольку стороны единичного квадрата первоначально параллельны и ранее было показано, что параллельные линии преобразуются снова в параллельные, то результирующая фигура является параллелограммом.

Влияние элементов а, b, с и d матрицы 2х2 может быть установлено отдельно. Элементы b и с, как видно из рис. 1.5, вызывают сдвиг исходного квадрата в направлениях y и x соответственно. Как отмечалось ранее, элементы а и d играют роль масштабных множителей. Таким образом, 2х2-матрица задает комбинацию сдвига и масштабирования.

Несложно определить также площадь параллелограмма А*В*С*D* из рис. 1.5, которую можно вычислить следующим образом:

 

Ap = (a + c)(b + d) -

1 2

(ab) -

1 2

(cd) -

c 2

(b + b + d) -

b 2

(c + a + c)

В результате получаем

 

Ap = ad - bc = det		a   b   c   d

Можно показать, что что площадь любого параллелограмма А_р, образованного путем преобразования квадрата, есть функция от определителя матрицы преобразования и связана с площадью исходного квадрата A_s простым отношением

 

А_р = A_s(ad - bс) = A_s det [T].

Фактически, так как площадь всей фигуры равна сумме площадей единичных квадратов, то площадь любой преобразованной фигуры А_t зависит от площади исходной фигуры A_i

 

A_t = A_i(ad - bc).

Это полезный способ определения площадей произвольных фигур.