1.12. Проецирование - геометрическая интерпретация однородных координат

Матрицу преобразования размером 3х3 для двумерных однородных координат можно разбить на четыре части

 

[T] =		a   b   ...   p c   d   ...   q ...   ...   ...   ... m   n   ...   s

Напомним, что a, b, с и d - коэффициенты масштабирования, вращения, отражения и сдвига соответственно. Элементы m и n задают перемещение. Установим величины р и q не равными 0. Какой эффект мы получим? В данном случае полезно рассмотреть геометрическую интерпретацию.

При p = q = 0 и s = 1 однородные координаты преобразованных векторов всегда равны h = 1. Геометрически данный результат интерпретируется как ограничение преобразования физической плоскостью h = 1.

Для иллюстрации эффекта преобразования при р и q, отличных от нуля, рассмотрим следующее выражение:

 

[X  Y  h] = [hx  hy  h] = [x  y  1]		1   0   p 0   1   q 0   0   1		= [x  y  (px + qy +1)]	(1.1)

Здесь X = hx, Y = hy и h = px + qy + 1. Преобразованный координатный вектор, выраженный в однородных координатах, лежит теперь в трехмерном пространстве, определенном как h = рх + qy + l. Это преобразование показано на рис. 1.6, где отрезок АВ, принадлежащий физической плоскости h = 1, преобразуется к CD со значением h <> 1, т.е. рХ + qY - h + 1 = 0.

 

 

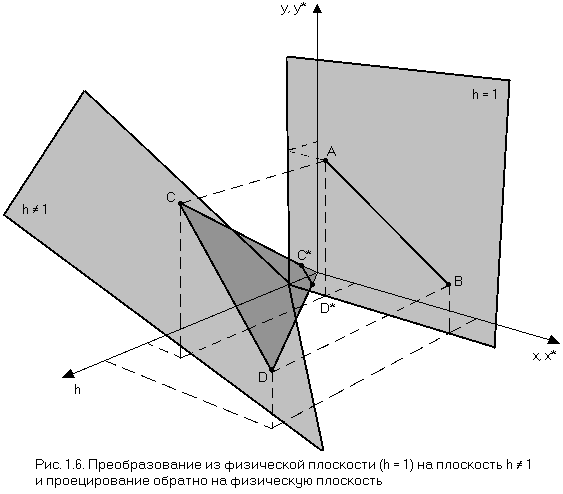
Однако представляют интерес результаты, принадлежащие физической плоскости с h = 1, которые можно получить путем геометрического проецирования прямой CD с плоскости h <> 1 обратно на плоскость h = 1 с использованием для этого проецирующих лучей, проходящих через начало координат. Из рис. 1.6, используя правило подобия треугольников, получим

 

x* =

X h

y* =

Y h

или в однородных координатах

 

[x*  y*  1] =		X h		Y h		1 h

После этого, нормализуя выражение (1.1) делением однородных координат на величину h, получаем

 

[x*  y*  1] =

X h

Y h

1 h

=

x px + qy + 1

y px + qy + 1

1

или

 

x* =

X h

=

x px + qy + 1

y* =

Y h

=

y px + qy + 1