2.8. Афинная и перспективная геометрия
К настоящему времени разработана математическая теория как для перспективной (начертательной), так и для аффинной геометрии. Теоремы аффинной геометрии идентичны теоремам геометрии Евклида. И в той и в другой науках важным понятием является параллелизм. В перспективной геометрии прямые в общем случае не параллельны.
Аффинное преобразование есть комбинация линейных преобразований, например поворота и последующего переноса. Для аффинного преобразования последний столбец в обобщенной 4х4-матрице равен [0 0 0 1]Т. В противном случае, преобразованная однородная координата h не равн единице и нет взаимно однозначного соответствия между афинным преобразованием и (4х4)-матричным оператором. Афинные преобразования образуют полезное подмножество билинейных преобразований, так как произведение двух аффинных преобразований также аффинно. Это свойство позволяет скомбинировать общее преобразование множества точек относительно произвольной системы координат при сохранении значения единицы для однородной координаты h.
Так как евклидова геометрия изучается в школах многие годы, то методы рисования и черчения, основывающиеся на евклидовой геометрии, стали стандартными методами графического сообщения. Хотя художниками и архитекторами часто используются перспективные виды для создания более реалистического изображения, в технической работе они используются редко из-за трудности их ручного конструирования. Однако при использовании для задания объекта однородных координат, аффинные и перспективные преобразования вычисляются одинаково легко.
И аффинные, и перспективные преобразования трехмерны, т.е. являются преобразованиями одного трехмерного пространства в другое. Однако для наблюдения результатов на двумерной поверхности требуется проецирование из трехмерного пространства в двумерное. Результат этого проецирования называется плоской геометрической проекцией. На рис. 2.2 изображена иерархия плоских геометрических проекций. Матрица проецирования из трехмерного пространства в двумерное всегда содержит столбец из нулей, следовательно, детерминант этого преобразования всегда равен нулю.
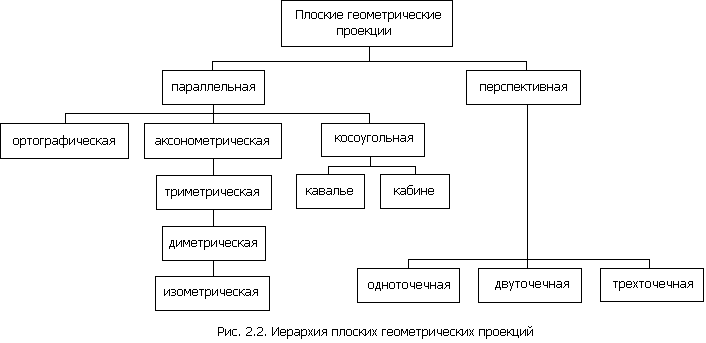
Плоские геометрические проекции объектов образуются пересечением прямых, называемых проекторами, с плоскостью, называемой плоскостью проекции. Проекторы - это прямые, проходящие через произвольную точку, называемую центром проекции, и каждую точку объекта. Если центр проекции расположен в конечной точке трехмерного пространства, получается перспективная проекция. Если центр расположен в бесконечности, то все проекторы параллельны и результат является параллельной проекцией. Плоские геометрические проекции составляют основу описательной геометрии. Неплоские и негеометрические проекции также полезны; они широки используются в картографии.