3.4. Общие уравнения конических сечений
Общий вид неявного уравнения второй степени
порождает различные двумерные кривые, называемые коническими сечениями. На рис. 3.2 изображены три вида конических сечений - парабола, гипербола и эллипс. Окружность - это частный случай эллипса. Определяя коэффициенты a, b, c, d, e и f, можно получить разные конические сечения. Если сечение задано относительно локальной системы координат и проходит через ее начало, то f = 0. Для того чтобы провести кривую через данные точки, используются граничные условия.
.gif)
Пусть с = 1, тогда сегмент кривой между двумя точками определяется пятью независимыми условиями, из которых вычисляются оставшиеся коэффициенты a, b, d, e и f. Например, можно указать положение крайних точек, наклон кривой в них и промежуточную точку на кривой.
Если b = 0, c = 1, то аналитическое представление кривой получается с помощью только четырех дополнительных условий, например положения концевых точек и наклона кривой в них. Кривая при а = 1, b = 0 и с = 1 еще проще
Тремя условиями для вычисления d, е и f могут быть две концевые точки и наклон кривой в одной из них или же две концевые точки и третья точка на кривой.
При а = b = с = 0 получается прямая линия. Ее уравнение
Конические сечения являются центральными - эллипс и гипербола или нецентральными - парабола. Кроме того, существует ряд вырожденных форм, которые все центральны.
Итак, уравнение представляет параболу при b2 - 4ac = 0 и центральное сечение при b2 - 4ac <> 0. Если сечение центрально и b2 - 4ac < 0, уратвнение представляет эллипс, а если b2 - 4ac > 0 - гиперболу.
| Невырожденные сечения | ||||
| Название | Уравнение | Условия | Тип | Чертеж |
| Эллипс | ax2 + by2 = k | k, a, b > 0 | Центральный | 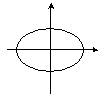 |
| Гипербола | ay2 + bx = 0 bx2 + ay = 0 |
b < 0 < k, a | Центральный | 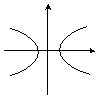 |
| Парабола | ax2 + by2 = k | k, a, b > 0 | Нецентральный | 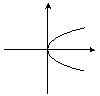 |
| Вырожденные сечения | ||||
| Пустое множество | ax2 + by2 = k | a, b < 0 < k | Центральный | Чертеж отсутствует |
| Точка | ax2 + by2 = 0 | a, b > 0 | Центральный | 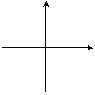 |
| Пара прямых | ax2 + by2 = 0 | b < 0 < a | Центральный | 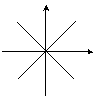 |
| Праллельные прямые | ax2 = k | k, a > 0 | Центральный | 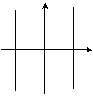 |
| Пустое множество | ax2 = k | a < 0 < k | Центральный | Чертеж отсутствует |
| Повторяющаяся прямая | ax2 = 0 | k, a, b > 0 | Центральный |  |